Fuzzy graph-schemes in pattern recognition © 1992 Dmitry A.Kazakov

to chapter two

3. Теория возможностей в задаче нечеткого обучения

3.1. Нечеткие события, классы и признаки

В данном разделе будет дана интерпретация понятий класса и признака с позиции нечеткости. В 3.1.1. будут введены понятие нечеткого признака как нечетко-значного отображения вероятностного пространства, и нечеткий аналог пространства признаков. В 3.1.2. рассмотрена проблема оценки условной вероятности нечеткого события, в 3.1.3. полученные оценки распространяются на пространство нечетких признаков.

Рассмотрим вероятностное пространство (Ω,σ(Ω),P), где Ω - непустое множество элементарных событий (мы будем считать его конечным); σ(Ω) - борелевское поле подмножеств Ω (σ(Ω) замкнуто относительно не более чем счетного числа операций объединения и дополнения); P - вероятностная мера.

Наблюдаемые нами явления, рассматриваемые, как элементарные исходы далеко не всегда независимы, как это предполагает вероятностная модель. Альтернативой вероятностного подхода является теория возможностей [Дю90], в которой элементарные события образуют цепочку вложенных друг в друга множеств. Оба подхода представляют собой полярные точки зрения на строение пространства элементарных исходов. Таким образом, вводимая нами нечеткость событий вызвана стремлением компенсировать неадекватность обоих моделей. Следует отметить, что нечеткость не есть прерогатива именно теории возможностей, просто ее аппарат более приспособлен для работы с нечеткими событиями, нежели аппарат теории вероятностей.

Нечетким событием мы будем называть нечеткое множество p:Ω→[0,1].

В теории нечетких множеств Заде (Zadeh) [Зад80, Коф82, Бор89, Мел90], нечеткое подмножество p данного четкого множества Ω задается своей функцией принадлежности, ставящей в соответствие каждому элементу базового множества Ω число из интервала [0,1]. Мы будем считать, что нечеткое множество и его функция принадлежности есть один и тот же объект. Операции объединения и пересечения вводятся, как max и min. Операция дополнения p как 1-p.

Нечеткое событие есть естественное обобщение понятия четкого события. Его вероятность (см. так же главу 1.):

Возможность нечеткого события p при условии нечеткого события q определяется как [Дю90]:

Необходимость:

Помимо вероятностной меры над пространством событий можно задать функцию распределения возможностей π [Дю90]. Функция π:Ω→[0,1] должна удовлетворять требованию нормальности, т.е. ω₀Ω  π(ω₀)=1. Ясно, что π можно рассматривать как нечеткое множество над Ω, тогда возможность и необходимость нечеткого события p вводятся как C(p|π) и N(p|π).

Противоположным событию p, является событие - дополнение p в смысле нечетких множеств:

Нечеткое событие p мы будем называть нормальным, если его функция принадлежности достигает 1: ω₀Ω  π(ω₀)=1. Для возможностей и необходимостей некоторых нечетких событий p, q и нормального события s справедливы следующие соотношения:

Как мы видим закон исключенного третьего выполняется лишь частично.

Таким образом, необходимость нечеткого события не превосходит его возможность.

Классы естественным образом можно представить как нечеткие события с пространством (Ω,σ(Ω),P). При этом, если функция принадлежности класса pⁱ:Ω→[0,1] принимает значения только 0 или 1, мы имеем обычный случай четкого класса [Вер85]. Следует отметить, что подобное представление класса неявно предполагает аддитивность образов, т.е. независимость степени уверенности в принадлежности классу или объекту данного элементарного события от остальных элементарных событий. Такая ситуация не всегда имеет место, например, при распознавании рукописных букв, когда в качестве пространства событий и пространства признаков выбирается растр изображения T, так как одни и те же пикселы растра могут быть частями различных букв.

На самом деле, в качестве пространства признаков здесь следует рассматривать, по крайней мере, 2^T - множество всех подмножеств растра T - или его часть [Шле89].

Собственно, модель нечетких классов призвана, помимо прочего, компенсировать неаддитивность четких классов. Она может оказаться продуктивной в том случае, когда перекрытие классов вследствии их неаддитивности становится почти полным, что делает их неразделимыми в четкой модели, тогда как в нечеткой, разделимости можно добиться за счет различия функций принадлежности. Однако, когда, как в предыдущем случае, неаддитивность носит структурный характер, следует менять признаки.

Так как вероятностное пространство (Ω,σ(Ω),P) обычно не доступно для непосредственного исследования, приходится иметь дело с пространством признаков.

В общем случае, нечеткий признак x_i принимает значения из некоторого множества D_i (будем считать его конечным). Если признак x_i нечеток, то для каждого элементарного события ωΩ мы располагаем не конкретным значением признака x_i(ω)D_i, но функцией принадлежности x_i(ω):D_i→[0,1]. Т.е. x_i(ω) - это нечеткое множество над D_i, а x_i(ω,d) - возможность того, что признак x_i принимает значение d на элементарном событии ω. Например, если Ω - множество видов животных, ω - конкретный вид - Homo Sapiens; x_i - признак «рост», то x_i(ω) - рост человека как вида (см. рис. 3.1.).

Рис. 3.1. Функция принадлежности x_i(ω)

С другой стороны, нечеткий признак x_i можно рассматривать как нечеткое множество над ΩD_i - x_i:ΩD_i→[0,1]. Аналогичный подход к распознаванию образов развивается в [Har75], с той только разницей, что признаки там рассматриваются как четкие бинарные отношения - x_i:ΩD→{0,1}.

3.1.1. Пространство нечетких признаков

Рассмотрим совокупность N нечетких признаков x_i {x_i:Ω→[0,1]^Di}. Пространством нечетких описаний мы будем называть множество N-мерных векторов с нечеткими координатами из _i [0,1]^Di ( _i). Образы, подлежащие распознаванию, являются элементами .

С другой стороны, совокупность нечетких признаков можно рассматривать как один признак x:Ω→[0,1]^D, где D = D_i - декартово произведение областей значений нечетких признаков. Пространством нечетких признаков мы будем называть множество =[0,1]^D - множество векторов с координатами из [0,1], индексируемыми элементами D.

Классическая вероятностная теория распознавания образов [Фук79] рассматривает признаки как случайные величины. Отметим, что не для всех из существуют прообразы x^-1(), т.е. x не действует на . Этот факт говорит о невозможности рассмотрения x как случайной величины во многих прикладных задачах.

Мы будем интерпретировать множества x(ω) как «фокальные элементы». [Дю90, Бор89], порождающие, согласно Шейферу (Shafer), верхнюю P^* и нижнюю P^* вероятности, представляющие собой оценки «истинной вероятности». P_x:

a

Следовательно каждому a мы можем поставить в соответствие два нечетких события:

a_*a^*, если множество x(ω) нормально при любом ω. Несовпадение a^* и a_* отражает тот факт, что в общем случае по признакам невозможно точно идентифицировать точку пространства элементарных событий. Множество a^* можно рассматривать как наименьшее нечеткое событие, связанное с элементом пространства признаков a. Соответственно, a_*- наибольшее нечеткое событие влекущее a.

В [Дю90] рассматривается вопрос построения меры возможностей по фокальным элементам. Нас же будет интересовать проблема оценки условных вероятностей нечетких событий по их образам в пространстве признаков .

3.1.2. Условные вероятности нечетких событий

Вероятность нечеткого события p:Ω→[0,1] в вероятностном пространстве (Ω,σ(Ω),P) определяется как (см. так же главу 1):

Если событие p-нечеткое, а q-четкое, то условная вероятность вводится обычным образом:

   , где

   - условная вероятностная мера

В том случае, когда q-нечетко, невозможно обеспечить выполнение обоих свойств условной вероятности:

и

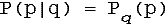
Действительно, условная вероятность предполагает, что нечеткое событие q свершилось. Но сама нечеткость этого события лишает нас возможности определить, что же именно имело место. Мы можем уверенно сказать, что состоялось событие, являющееся четким подмножеством q: {ω|q(ω)=1}. С меньшей степенью уверенности можно утверждать, что имело место событие {ω|q(ω)0.5} и т.п. Это наводит на мысль об использовании α-срезов нечеткого множества q.

Рассмотрим α-срезы q [Дю90, Коф82, Бор89]:

α-срезы - четкие множества, следовательно для них можно определить условные вероятности P(p|q_α). Постараемся их оценить:

Это дает нам основание считать, что при корректном определении условной вероятности нечетких событий P(p|q)C(p|q). Аналогично, учитывая, что

получим:

3.1.3. Признаки нечетких событий

Функция x(ω):D→[0,1] естественным образом вводит распределение возможностей над D. x(ω,d) есть возможность того, что признак принимает значение d на элементарном событии ωΩ. Соответственно, для произвольного события (возможно нечеткого) p:Ω→[0,1] распределение возможностей x(p):D→[0,1] будет иметь вид:

Нечеткое множество x(p) есть образ нечеткого события p в пространстве нечетких признаков .

Пусть теперь p,q[0,1]^Ω - пара нечетких событий, тогда

при условии нормальности признаков, т.е. когда

С другой стороны:

Отметим, что

Таким образом, мы располагаем соотношениями

позволяющими оценивать величины N(p|q) и C(p|q) по образам событий p и q в пространстве признаков . Ошибка в оценке сверху для возможности и снизу - для необходимости приводит к «размыванию». нечеткого события. В этом заключается одно из преимуществ теории возможностей - естественность представления данных независимо от полноты информации. В теории вероятностей знание вероятности некоторого события предполагает, обладание всей полнотой информации о нем. Но если информация неполна, то какую вероятность следует приписать событию? Ни 0 ни 0.5 ни 1! Обычно, дополнительно вводятся эмпирические меры полноты информации, такие как факторы уверенности экспертной системы MYCIN [Экс87] (confidence factor) и т.п. В теории возможностей отсутствие информации представляется естественным образом. Например в нашем случае:

означает полную неопределенность признаков нечеткого события - все значения признаков полностью возможны, но ни одно не необходимо.

Предположим теперь, что p=p₁p₂, тогда

Аналогично, для p=p₁p₂:

Эти соотношения позволяют манипулировать с образами нечетких событий, не нарушая истинности оценок.

3.1.4. Пространство классов

Пусть {p^j} - множество классов, возможно нечетких и пересекающихся: p^j:Ω→[0,1]. Задачей классификации объекта q:Ω→[0,1] (в общем случае, нечеткого и неточечного) обычно считается определение условных вероятностей {P(p^j|q)} [Ту78, Вер85]. Величина P(p^j|q) есть вероятность того, что объект q принадлежит классу p^j.

В дальнейшем мы будем считать, что нечеткие множества {p^j} и q - нормальны. Говоря неформальным языком, это означает, что и классы и классифицируемые объекты должны быть не менее чем точечными, т.е. содержать в качестве подмножества хотя бы одно элементарное событие из Ω.

Ранее было показано, что P(p^j|q) не определено для нечеткого q - его можно лишь оценить по образам классов pj и объекта q в пространстве признаков . Поэтому под результатом классификации мы будем понимать не распределение по классам условных вероятностей P(p^j|q), но распределение возможностей и необходимостей, т.е. пару нечетких множеств над множеством классов {p^j}_1,..,M:

каждое из которых представляет собой точку из пространства классов . Классифицирующее правило мы определим как функцию, отображающую пространство нечетких описаний в пространство нечетких решений ²:

f : →²

или

  , где f_C : → ;  f_N : →

Функция f_C показывает насколько возможна принадлежность классифицируемого объекта классам, другими словами, в какой степени непусто пересечение классов и объекта.

Функция f_N показывает насколько необходимо входит объект в классы, т.е. в какой степени он вложен в каждый из классов.

В литературе по нечетким множествам условная необходимость, определяющая величину f_N называется нечеткой импликацией [Мал91].

3.2. Задача нечеткого обучения

В этом разделе будет сформулирована задача нечеткого обучения с учителем. В 3.2.1. дается нечеткий аналог метода эталонов [Тим83] - решающее правило типа «перечисления» и исследуются его свойства: показывается, что существуют нечеткие «образы» классов, определяющие результат классификации, далее для образов классов вводится метрика и доказывается, что расстояние между образами двух классов равняется максимальному расхождению классификаций основанных на них решающих правил (Теоремы 3.2.1 и 3.2.2). В конце раздела доказывается, что поведение правила типа «перечисления» полностью определяется тем, как оно классифицирует точечные объекты (Теоремы 3.2.3 и 3.2.4).

Пусть:

1º (Ω,σ(Ω),P) - вероятностноепространствонадконечным Ω.

2º {x_i} - множество нечетких признаков с совместным распределением x:Ω→[0,1]^D, определяющим пространство нечетких признаков =[0,1]^D, где D= D_i - декартово произведение областей значений признаков, и для любого нечеткого события q[0,1]^Ω его образ в есть x(q):

Пока признаки рассматриваются, как один совокупный признак, пространство нечетких описаний совпадает с проистраниством нечетких признаков .

Мы будем требовать нормальности признаков, т.е. нормальности нечеткого множества x(ω) при любом ωΩ.

Нормальность x(ω) означает, что каждое элементарное событие ω имеет в качестве своего образа x({ω}) x(ω) - нормальное нечеткое множество в пространстве признаков . Другими словами, в каждом элементарном событии хотя бы одно значение признаков полностью возможно.

3º {p^j} - множество нечетких классов p^j:Ω→[0,1]. Классы должны быть нормальны.

Нормальность классов означает, что каждый класс содержит хотя бы одно элементарное событие с возможностью 1.

Множество классов задает пространство нечетких классов и пространство нечетких решений ²:

4º

- обучающее множество, то есть множество пар, где первый элемент каждой пары - образы нечеткого события и его дополнения , a второй - класс, к которому это событие отнесено. Мы будем назМы будем называть первый элемент каждой такой пары - обучающим примером.

Требуется:

Построить по L нечеткое решающее правило G_L:→², оптимальное в некотором смысле. Мы не будем уточнять слово «оптимальное», отметим лишь, что целые области в теории распознавания образов порождаются различными вариантами его толкования [Ту78, Вер85, Фук79].

Возможна и более общая постановка задачи, когда каждый обучающий пример содержит указание не на один класс, но на распределение возможностей и необходимостей принадлежности его классам:

4º'

, где

нечеткие множества

задают распределения возможностей и необходимостей:

есть возможность, а

- необходимость принадлежности данного обучающего примера классу p^j.

Такая постановка задачи соответствует случаю, когда «учитель». не выбирает примеры из классов, а наблюдает самопроизвольно происходящие события, оценивая их признаки и классифицируя их с помощью идеального классификатора, который в силу нечеткости событий и возможного пересечения классов не может быть уверен на все 100%.

Фактически результат работы идеального классификатора и есть

:

Это означает, что верхнюю P^*(p^j|q^l) и нижнюю P_*(p^j|q^l) вероятности принадлежности прообраза обучающего примера классу можно принять равными:

Следовательно, можно построить пару нечетких множеств, оценивающих идеальный обучающий пример, который строго входит в класс p^j. Это делается тем же способом, каким строятся функции принадлежности нечетких событий по неточным статистическим данным [Дю90]:

  , где

Таким образом задачу 4º' можно свести к задаче 4º, введя в обучающее множество M (по числу классов) новых обучающих примеров вместо каждого старого. Причем каждый новый пример относится строго к одному классу:

3.2.1. Классифицирующее правило типа «перечисления».

Обучающее множество L есть многозначная функция, ставящая в соответствие каждому обучающему примеру один или несколько классов:

Рассмотрим множество прообразов обучающих примеров, относимых к классу p^j:

Множество Q_j содержит в себе прообразы всех обучающих примеров, относимых к классу p^j, следовательно, при исчерпывающем обучающем множестве можно предположить, что:

Следовательно:

и

Множества и представляют собой верхнюю и нижнюю оценки образа класса x(p^j) и его дополнения. Соответственно y:

Таким образом, мы построили примитивное решающее правило E:→² типа «перечисления»:

Хотя правило E и демонстрирует некоторую гибкость, уже в силу своей нечеткости, напрямую оно может использоваться только в том случае, когда обучающее множество является исчерпывающим.

Исследуем поведение правила типа перечисления. Для этого введем в пространстве признаков метрику следующего вида:

Легко убедиться в выполнении аксиом расстояния:

1. d(a,b)=0 a=b

2. d(a,b)=d(b,a)

3. d(a,b)=

Оценим насколько отличаются пары возможность - необходимость для различных классов pⁱ и p^j, т.е. величины:

и

Теорема 3.2.1. (доказательство)

Теорема 3.2.2. (доказательство)

Теоремы 3.2.1 и 3.2.2 показывают, что если образы классов pⁱ и p^j отличаются не более, чем на величину T, то возможности и необходимости принадлежности произвольного объекта этим классам, оцененные решающим правилом типа «перечисления», расходятся не более, чем на T.

Посмотрим как правило E классифицирует точки пространства описаний . Пусть δ_d- точечное множество, определяемое следующим образом:

Теорема 3.2.3. (доказательство)

Следствием этой теоремы является то, что если в обучающем множестве не представлено некоторое значение признаков dD, т.е.

  , то

Другими словами, вне множества обучающих примеров правило E выдает «ложь» для всех классов, что можно рассматривать как отказ от классификации.

Теорема 3.2.4. (доказательство)

Пусть E¹ и E² - правила типа «перечисления» такие, что dD  E¹(δ_d)=E²(δ_d) , тогда y E¹(y)=E²(y).

Эта теорема показывает, что для установления факта тождественности двух правил типа «перечисления» достаточно убедиться, что они совпадают на точечных элементах пространства описаний .

3.3. Проблема зависимости признаков

В данном разделе рассматривается проблема зависимости нечетких признаков. Доказывается (Теорема 3.3.1) оценка для условных событий в случае нескольких признаков. Далее показывается, что эта оценка улучшается, если при определении значения некоторого признака используется информация о значениях ранее определенных признаков (Теоремы 3.3.2, 3.3.3, 3.3.4, 3.3.5, 3.3.6).

В классической теории распознавания образов проблема выбора независимых признаков играет очень большую роль [Ту78, Фук79]. Независимость признаков является основным условием разложимости пространства признаков в прямое произведение подпространств отдельных признаков. Мы рассмотрим этот вопрос для случая нечетких признаков.

Пусть, как и ранее, задано множество нечетких признаков с областями значений D_i, а x:ΩD→[0,1] - их совместная функция распределения возможностей, где D= D_i - декартово произведение областей значений признаков, т.е. dD есть

  , где d_iD_i .

Определим проекцию i-го признака как нечеткое множество x_i:ΩD_i→[0,1]

Проекция x_i может рассматриваться как нечеткий признак, причем для нечеткого события q[0,1]^Ω

Т.е. x_i(q) - не что иное, как распределение возможностей значений i-го признака на событии q.

Очевидно, что dD x(q)(d) x_i(q)(d_i), следовательно

 .

Если рассматривать цилиндрические продолжения x_i(q) на все , т.е.

определяемые, как

  , то

Иными словами, образ нечеткого события q в пространстве признаков вложен в декартово произведение распределений возможностей признаков x_i события q.

Мы будем называть совокупность признаков {x_i} независимыми признаками, если их совместная функция распределения возможностей представима в виде:

Отметим явную аналогию с независимыми случайными величинами в теории вероятностей [Кра75].

Обычной является ситуация, когда признаки вводятся эмпирически. При этом, проблема установления факта зависимости или независимости признаков усложняется как тем, что обучающее множество часто недостаточно представительно для оценки статистических гипотез, так и неприменимостью классической теории оценки гипотез для нечетких признаков. Разработка же теории «нечеткой статистики» в настоящее время лишь начинается [Кле86, Цук86].

Однако, для теории возможностей независимость признаков не играет той роли как в теории вероятностей. Дальнейшие результаты имеют вид оценок, которые справедливы как для зависимых так и для независимых совокупностей признаков.

Теорема 3.3.1 (доказательство)

p,q[0,1]^Ω

Оценки Теоремы 3.3.1 можно усилить, если при определении значения признака x_i учитывать «предысторию» - значения признаков x₁,..,x_i-1. Пусть

- реализации признаков {x_k}_k<i

Тогда возможность того, что признак x_i принимает значение tD_i на элементарном событии ωΩ при условии y есть по-определению:

Соответственно, образом нечеткого события q[0,1]^Ω при условии y будет:

Так как

то

Рассмотрим свойства условного распределения возможностей.

Теорема 3.3.2. (доказательство)

Теорема 3.3.3. (доказательство)

Теорема 3.3.4. (доказательство)

Теорема 3.3.5. (доказательство)

Следствие: если

то

Однако, в общем случае, мы имеем лишь неравенство, о чем говорит нижеследующая теорема:

Теорема 3.3.6. (доказательство)

3.4. Задача нечеткого обучения для нескольких признаков

В этом разделе мы сформулируем задачу нечеткого обучения с учителем для случая нескольких признаков. Будет сконструировано и исследовано правило типа «перечисления» для этого случая (Теорема 3.4.1). Далее рассматривается вопрос об условиях эквивалентности обучающих множеств при изменении признаков 3.4.1. Вводится понятие эквивалентности обучающих множеств и доказывается основной результат (Теорема 3.4.2). Затем для случая нескольких признаков обобщаются результаты раздела 3.2. (Теоремы 3.4.3 и 3.4.4).

При наличии нескольких нечетких признаков {x_i} пространство нечетких описаний становится прямым произведением признаковых подпространств:

  ,

где _i=[0,1]^Di.

Образом нечеткого события q[0,1]^Ω в будет вектор:

   , где x_i(q)_i - образ q в _i.

Т.е. мы имеем обычный для теории распознавания образов вектор признаков [Ту78, Вер85]. Правда, в качестве его координат выступают, в общем случае, нечеткие множества.

Соответственно, обучающее множество принимает вид:

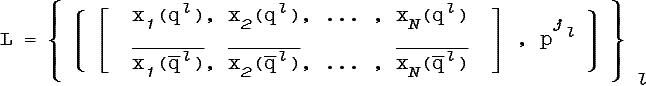
По обучающему множеству L мы можем легко построить решающее правило типа «перечисления», которое с учетом полученных ранее результатов, будет следующим:

   , где

Как и ранее Q_j - множество прообразов обучающих примеров, относимых обучающим множеством к классу p^j.

Важным моментом является то, что пространство нечетких описаниий заменено здесь на пространство нечетких признаков , т.е. правило типа «перечисления» выдает одинаковые результаты для классов эквивалентности в :

Различие между пространствами и состоит в том, что

, а

если - пространство векторов с нечеткими координатами, то - пространство нечетких подмножеств пространства четких векторов.

Классифицирующее правило E является эталоном в том смысле, что любое другое правило должно вести себя подобно E на множестве обучающих примеров.

Исследуем поведение правила типа «перечисления».

Теорема 3.4.1. (доказательство)

где

К сожалению, для оценки необходимостей правилом E невозможно получить аналогичное выражение.

3.4.1. Эквивалентность обучающих множеств

Выбор признаков, в достаточной степени произволен. Поэтому важно установить, какие изменения обучающего множества и пространства признаков не влияют на результат классификации.

Мы будем называть пространства нечетких описаний ¹ и ² эквивалентными и писать ¹~², если существует биекция h, связывающая области значений признаков {x¹_i} и {x²_i}:

h:D¹→D² , где

Биекция h порождает биекцию , связывающую ¹ и ²:

:¹→² ,  где

¹ [0,1]  ;  ² [0,1]   и

(¹) [0,1]^h().

Например, если ¹¹ - нечеткое множество над D¹, то (¹)² есть нечеткое множество над D², причем

[(¹)] (d²) ¹(h^-1 (d²)) или, что то же самое

[(¹)] (h(d¹)) ¹(d¹).

Мы будем говорить, что y¹¹ эквивалентно y²² и писать y¹~y², если:

1. ¹ эквивалентно ²;

2. (¹) = ².

Графически это можно изобразить, как показано на рис. 3.3.

Рис3.3..Эквивалентность двух пространств описаний

Если d ( (¹), ²) T, то мы будем говорить, что y¹ и y² эквивалентны с точностью до T: y¹ y².

Два обучающих множества L¹ и L² будем называть эквивалентными с точностью до T, и писать L¹ L², если

1. ¹ = ² = - одно и то же множество классов;

2. ^{1 2}- пространства признаков эквивалентны;

3.

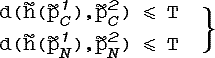
Формально это можно записать, как и..

Теорема 3.4.2. (доказательство)

L¹ L² y¹ y²  d(E¹(y¹), E¹(y²)) T

Данная теорема показывает, что эквивалентные с точностью до T обучающие множества порождают правила типа «перечисления», отличающиеся не более, чем на величину T.

Теорема 3.4.3. (доказательство)

где

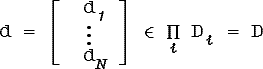
Теорема 3.4.4. (доказательство)

Эта теорема показывает, что для объектов, не представленных во множестве обучающих примеров (α-срез T их пересечения пуст), правило типа «перечисления» выдает возможности не превышающие величину T. Т.е. правило типа «перечисления» ничего «от себя» не добавляет - отсутствует элемент обучения. Когда соответствующего примера в обучающем множестве нет, следует «отказ». Отсюда, непосредственное использование его в качестве классифицирующего правила возможно только при исчерпывающем множестве обучающих примеров, т.е. множестве, покрывающем всю область значений признаков D.

3.5. Выводы

1. Предложенная постановка задачи нечеткого обучения с учителем, в частности трактовка признаков, как нечетко-значных отображений, позволяет описывать более общий класс задач, нежели при обычном - статистическом подходе.

2. Для зависимых признаков возможно их раздельное использование в решающем правиле, с последующим объединением частных ответов в единый блок. При этом, размытость классификации может быть уменьшена при последовательной проверке признаков, если на каждом шаге учитывается информация о значениях признаков, опрошенных на предыдущих шагах.

3. В предложенном классе классифицирующих правил каждое правило может быть полностью описано набором «образов» классов.

4. Возможна версификация признаков и обучающего множества инвариантная к классифицирующему правилу.

to chapter four