Fuzzy graph-schemes in pattern recognition © 1992 Dmitry A.Kazakov

to chapter three

4. Нечеткие граф-схемы

Для решения задачи нечеткого обучения мы будем использовать аппарат нечетких граф-схем.

4.1. Нечеткие графы и граф-схемы

В этом разделе будет обобщено на нечеткий случай понятие граф-схемы. В 4.1.1. дается определение нечеткой граф-схемы. Далее в 4.1.2. рассматривается поведение граф-схемы как решающего правила. Доказывается эквивалентность граф-схемы и «образов классов», введенных в разделе 3.3. (Теорема 4.1.1). Показывается аддитивность граф-схемы по объединению (Теорема 4.1.2) и условие доминирования возможности над необходимостью при использовании граф-схем (Теорема 4.1.3). В 4.1.4. предлагается метод приведения нечеткой граф-схемы к каноническому виду (с четкими дугами) и доказывается соответствующая теорема (Теорема 4.1.4).

Граф Бержа [Оре80] вводится как бинарное отношение над множеством вершин E - G:EE→{0,1}. Две вершины A,BE графа G связаы дугой тогда и только тогда, когда G(A,B)=1.

Нечеткий граф Бержа [Коф82] естественным образом обобщает понятие четкого графа. Нечеткий граф Бержа есть нечеткое бинарное отношение над множеством вершин E - G:EE→[0,1]. Совершенно очевидно, что нечеткий граф представляет собой нечеткое множество над E².

Определим композиции нечетких отношений:

R:E₁E₂→[0,1], S:E₂E₃→[0,1]

-композиция: SR:E₁E₃→[0,1]

AE₁ CE₃

В [Коф82] рассматривается º-композиция, аналогичная приведенной нами -композиции.

-композиция: SR:E₁E₃→[0,1]

AE₁ CE₃

Очевидно, что

Введем обозначение для r-раз и -композиций нечеткого отношения R (легко видеть, что и -композиции ассоциативны по отношению к самим себе):

При этом,

A,B

   

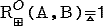
Путем T, длины r в нечетком графе G называется последовательность вершин: T={A_i}, где A_iE, а i=0,..,r.

С путем T можно связать пару величин:

и

В [Коф82] C_G(T) называется силой пути Т. По аналогии, N_G(T) можно назвать слабостью пути.

Ясно, что

и N_G(T) C_G(T).

Можно ввести понятия сильнейшего и слабейшего путей из вершины A в вершину B длины r. Сильнейший путь из A в B длины rесть такой путь, что для любого другого пути T той же длины C_G() C_G(T). Аналогично, - слабейший путь, если N_G() N_G(T). Отметим, что в дополнении графа G и меняются местами: () (T) и () (T).

В [Коф82] доказывается замечательный результат:

Аналогично:

Транзитивными замыканиями нечеткого отношения G называются нечеткие отношения G и G, определяемые как

В силу монотонности и ограниченности и G и G всегда существуют.

Легко убедиться, что для любых двух вершин A и B существуют сильнейший T_C и слабейший T_N пути такие, что:

C_G(T_C) = G(A,B)   и   N_G(T_N) = G(A,B)

Действительно, при длине пути, большей числа паросочетаний вершин графа, отрезки пути начинают повторяться,  не внося дальнейшего вклада в силу или слабость пути. То есть существует такое r, что t>r и .

4.1.1. Нечеткие граф-схемы

Четкие граф-схемы рассматриваются в работах [Тан74, Бл87, Орл82]. Мы обобщим понятие граф-схемы применительно к теории возможностей и теории нечетких множеств.

Рассмотрим функцию, ставящую в соответствие каждому вектору y из пространства нечетких описаний N признаков нечеткий граф G с вершинами из множества E:

y   G:EE→[0,1]

Причем, потребуем выполнения следующих условий.

1. Множество вершин E состоит из N+1 непересекающихся подмножеств:

Каждое E_i при iN соответствует признаку x_i: вершины из E_i «проверяют» признак x_i. Множество E₁ состоит из одной вершины S: E₁={S}. E_N+1 есть множество классов: E_N+1={p^j}.

2. При любом значении y

a. Вершина S - начальная: AE G(A,S)=0;

b. Дуги, исходящие из E_i (iN) входят в вершины E_k:

AE_i BE_k ik G(A,B)=0

c. Вершины {p^j} - конечные

BE  G(p^j,B)=0

Таким образом, G суть N+1 хроматический граф [Оре80].

3. Вес дуги, исходящей из вершины AE_i (iN) и входящей в вершину BE, определяется некоторым нечетким множеством p_AB[0,1]^Di, связываемым с A и B:

Подобную функцию мы будем называть нечеткой граф-схемой возможностей и изображать в виде графа с вершинами, связанными взвешенными величинами p_AB дугами, как показано на рис. 4.1.

Рис. 4.1. Дуга граф-схемы

Нечеткая граф-схема необходимостей вводится, как функция, ставящая в соответствие y нечеткий граф G, дополнение которого удовлетворяет перечисленным выше условиям. Т.е. дополнение нечеткой граф-схемы необходимостей есть нечеткая граф-схема возможностей, веса дуг которой являются дополнениями весов соответствующих дуг в исходной граф-схеме.

Граф-схемой вообще, мы будем называть пару нечетких граф-схем - возможностей и необходимостей:

G = { G_C ; G_N} :   y  G^y = { G ; G } .

Мы будем говорить, что дуга в граф-схеме возможностей отсутствует, если ее вес - пустое подмножество D_i: p_AB=Ø. Аналогично, в граф-схеме необходимостей дуга опускается, если ее вес есть D_i.

Можно отметить аналогию, между граф-схемой возможностей и электрической схемой, составленной из сопротивлений, с одной стороны, и, между граф-схемой необходимостей и электрической схемой из проводимостей, с другой.

4.1.2. Граф-схема, как решающее правило

Рассмотрим транзитивные замыкания нечетких графов G и G при фиксированном y:

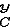
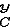
(G) = G    GG   GGG   ...

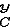
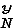
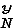
(G) = G  GG   GGG   ...

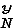
Можно ввести решающее правило G:→²:

По теореме о сильнейшем пути (см.[Коф82]):

Теорема 4.1.1. (доказательство)

  такие, что

q.e.d.

Очевидно, что справедливо и обратное утверждение, т.е. по любым {} и {} можно построить соответствующую им граф-схему.

Таким образом, граф-схема полностью описывается нечеткими множествами {} и {}. Где можно рассматривать как верхнюю оценку классифицирующим правилом G образа класса p^j. Аналогично, - нижняя оценка.

Теорема 4.1.2. (доказательство)

x,y,z

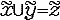
G_C(x) G_C(y) = G_C(z) & G_N(x) G_N(y) = G_N(z)

Теорема 4.1.3. (доказательство)

y нормального по всем y_i,

G_N(y) G_C(y) j

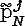
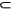
Решающее правило типа «перечисления»

может быть представлено в виде граф-схемы, для которой каждой точке dD и каждому классу p^j соответствует в граф-схемах возможностей и необходимостей путь из начальной вершины S в вершину класса p^j (см. рис. 4.2.).

Рис. 4.2. Граф-схемы эквивалентные правилу типа «перечисления»

Здесь α·δ_d обозначает точечное нечеткое множество вида:

Так как вдоль данного пути в граф-схеме возможностей

то

Аналогично для граф-схемы необходимостей:

4.1.3. Граф-схемы и нечеткие деревья решений

Нечеткие деревья решений широко используются в теории распознавания и классификации [Cha77]. Нечеткое дерево решений - это функция, ставящая в соответствие вектору значений нечетких признаков y[0,1]^N нечеткий граф определенного вида (обычно, дерево), веса дуг которого есть координаты вектора y.

Граф-схемы, с одной стороны, обобщают нечеткие деревья решений, так как веса дуг определяются более сложными функциями значений нечетких признаков. С другой стороны, граф-схема порождает пару нечетких графов: граф возможностей, собирающий свидетельства PRO и граф необходимостей, дополнение которого собирает свидетельства CONTRA.

Ценой определенного усложнения любая граф схема может быть преобразована в пару нечетких деревьев решений, что мы сейчас и продемонстрируем.

4.1.4. Граф-схемы с четкими дугами

Дугу граф-схемы возможностей G_C, проверяющую i-й признак (см. рис. 4.3.) мы будем называть четкой, если p_C - точечное четкое подмножество D_i, т.е.

Рис 4.3. Дуга  граф-схемы,  проверяющая i-й признак

Для четкой дуги

Аналогично, дугу p_N граф-схемы необходимостей мы будем называть четкой, если ее дополнение - точечное четкое подмножество D_i:

и, следовательно:

Если все дуги граф-схемы - четкие, то очевидно, что G_C и суть нечеткие деревья решений.

Рассмотрим процедуру преобразования обучающего множества L¹ к такому виду, что правило типа «перечисления» будет допускать реализацию в виде нечетких деревьев решений.

Построим обучающее множество L², в котором каждому обучающему примеру из L₁ будет соответствовать усеченный обучающий пример вида:

Усечение обучающих примеров до уровня T позволяет сократить количество дуг граф-схемы. Так как

и

то следовательно L¹ L². Введем теперь вырожденный признак x^N+1, принимающий лишь одно значение 1 (т.е. D^N+1={1}). Построим граф-схему в которой для каждого dD пути в класс p^j примут вид, показанные на рис. 4.4.

Рис. 4.4. Дуги четкой граф-схемы

Так как

и

то      и      , т.е.

L² ~ L³, а значит, L¹ L³. В построенных граф-схемах возможностей и необходимостей все дуги, проверяющие признаки x₁,x₂,...,x_N - четкие, признак x_N+11, следовательно G_C и дополнение G_N могут быть представлены нечеткими деревьями решений.

Классифицируемые объекты также могут быть преобразованы к виду, когда первые N признаков задаются четкими множествами, а вся нечеткость сводится в N+1-й признак.

Для объекта y построим множества y_d³ для dD:

Следовательно:

т.е. имеет место следующая теорема

Теорема 4.1.4. (доказательство)

Таким образом, первые N слоев граф-схемы, проверяющие признаки с первого по N-й могут быть четкими, что существенно упрощает программную реализацию.

4.2. Обучение

В данном разделе будет рассмотрена задача нечеткого обучения с учителем. Предлагается метрика для нечеткого аналога правила ближайшего соседа и рассматриваются свойства соответствующего классификатора (Теоремы 4.2.1 и 4.2.2). Далее в 4.2.1. предлагается алгоритм построения нечеткой граф-схемы, реализующей данный классификатор.

Как уже отмечалось ранее, по обучающему множеству L можно построить верхнюю и нижнюю оценки классов p^j:

и

(d) есть возможность принадлежности точки d образу класса pj. С этой точки зрения обучение есть увеличение в соответствии с некоторыми априорными знаниями о структуре образа класса. Т.е. цель обучения - восполнение неполноты обучающего множества, покрывающего не все возможные ситуации.

В [Экс87] рассматриваются следующие цели обучения:

• Расширение круга решаемых задач
• Выдача более точных результатов
• Получение ответов с меньшими затратами
• Упрощение уже имеющихся знаний

Так как априорная информация о классах носит, обычно предположительный (возможностный) характер, то увеличение вряд ли оправдано, ведь (d) - необходимость принадлежности d образу класса p^j .

Можно представить себе случай, когда априорная информация имеется не тоько о классах, но и о их дополнениях - обучение на отритцательных примерах. Тогда в процессе обучения должно уменьшаться.

Для общности рассуждений рассмотрим набор порогов {T_i}, где каждый порог T_i[0,1] соответствует некоторому признаку x_i. Пусть теперь a - некоторая точка из области значений признаков D.

Мы будем говорить, что a представлено в обучающем множестве L, если

q x_i(q)(a_i) T_i  ,  т.е.

Множество представленных в L элементов D мы будем обозначать как D_L:

Теорема 4.2.1. (доказательство)

Как мы уже отмечали ранее, целью обучения является увеличение множества образов классов таким образом, чтобы оно покрывало все точки D. Иными словами, необходимо изменить поведение классифицирующего правила в точках непредставленных в обучающем множестве.

Метризуем множество значений признаков D. Пусть области значений каждого из признаков x_i метризованы и d_i- соответствующие метрики. Если «естественного» расстояния для значений признака x_i нет, то можно ввести такую метрику:

Пусть ØD_i- диаметр D_i:

Тогда метрика D может иметь вид:

Аксиомы рассстояния:

1. d(a,b) = 0 i d_i(a_i,b_i) = 0 i a_i=b_i a=b

2. d(a,b) = d(b,a) i d(a_i,b_i) = d(b_i,a_i)

3. d(a,b) d(a,c) + d(c,b) i d_i(a_i,b_i) d_i(a_i,c_i)+d_i(c_i,b_i)

Построим множество следующим образом:

т.е. bD_L d(a,å) d(a,b). Можно сказать, что - наилучшее в смысле d продолжение множества D_L на все D.

Теорема 4.2.2. (доказательство)

aD_L

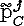
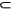
и при равных T_i

Очевидно, что если все пороги T_i=0, то =, т.е. обучение отсутствует. Вообще смысл порога T_i состоит в указании наименьшего уровня возможности принадлежности точек области значений признака x_i классам.

4.2.1. Алгоритм построения нечеткой граф-схемы

Рассмотрим, как строится граф-схема возможностей по обучающему множеству L.

Алгоритмы построения четких граф-схем можно найти в [Тан74, Орл82, Бл87].

1. Заменим в обучающем множестве величины x_i(q) на x_i(q)x_i(q)T_i , как показано на рис. 4.5.

Рис. 4.5. Усечение обучающего примера

2. Построим новое обучающее множество с четкими обучающими примерами, как мы это делали в предыдущем разделе. В этом множестве каждому обучающему примеру из L будет соответствовать

новых примеров вида:

где часть, соответствующая необходимостям нас не интересует, т.к. мы будем строить граф-схему возможностей, и

Если задача обучения содержит взвешенные обучающие примеры (4º'), то возможность того, что данный обучающий пример относится к классу p^j умножается на Min:

3. В качестве конечных узлов граф-схемы избираются классы pj. Далее обучающее множество последовательно свертывается по количеству признаков от n=N+1 до n=0.

4. Во множестве обучающих примеров выделяются классы эквивалентности, состоящие из примеров, первые n-1 значений признаков которых совпадают.

5. При n=N+1 для каждого класса эквивалентности строится узел с дугами, ведущими в классы, взвешенными наибольшими значениями признака x_N+1 для данного класса.

6. При nN возможны следующие варианты:

a. Все обучающие примеры из класса эквивалентности соответствуют одному классу. В этом случае ничего не делается.

b. Для каждого класса строится дуга, исходящая из нового узла. Веса всех дуг - объединение значений признака xn для всех обучающих примеров, входящих в класс эквивалентности. Если некоторые точки D_n (области значений признака x_n) не покрываются объединением весов дуг, то эти точки включаются в веса дуг, ближайших к ним по метрике d_n. Т.е. выбирается ближайшая точка из D_n, в которой функция принадлежности веса некоторой дуги не 0. В эту дугу и включается непокрытая точка, причем, значение функции принадлежности которой в этой точке принимается равным значению в ближайшей к ней точке. Например, если D_n={1,2,3,4}, то результат такой операции будет соответствовать, показанному на рис. 4.6.

Рис. 4.6. Преобразование дуг граф-схемы

Узлы с одинаковыми дугами, проверяющие один и тот же признак, объединяются. Эта операция превращает граф-схему в граф более общего вида нежели дерево.

7. Строится новое обучающее множество, в котором каждому классу эквивалентности соответствует один обучающий пример пример с n-1 признаком. В качестве классов новым обучающим примерам назначаются либо реальные классы, либо сгенерированные узлы. Новое обучающее множество непротиворечиво и содержит n-1 признак. Далее мы переходим к пункту 4.

Граф-схема необходимостей строится аналогичным образом:

1. Усечение обучающих примеров:

2. Новое обучающее множество:

3. p^j- конечные узлы

4. Выделяются классы эквивалентности

5. При n=N+1 строится узел с дугами, взвешенными наибольшими значениями признака xN+1.

6. Если обучение по отрицательным примерам не требуется, то узел генерируется в любом случае. Дуги взвешиваются дополнениями объединений значений признака x_n. В противном случае, действия те же, что и для алгоритма построения граф-схемы возможностей, за исключением того, что покрытие всех возможных значений признака соответствует не равенству объединения весов дуг D_n, на равенству Ø их пересечения.

7. Строим новое обучающее множество и переходим к пункту 4.

Формально говоря, граф-схема необходимостей строится в точности так же, как и граф-схема возможностей, за исключением того, что веса всех дуг, кроме тех, что исходят из узлов, проверяющих признак x_N+1, инвертируются.

4.3. Преобразование исходных данных

В данном разделе рассматриваются различные вопросы, связанные с преобразованием признаков. В 4.3.1. предлагается бинаризовать признаки, а в 4.3.2. излагаются необходимые изменения алгоритма построения нечеткой граф-схемы в случае бинаризации линейно-упорядоченных признаков: вводится понятие линейно-упорядоченного нечеткого признака, рассматривается метрика для правила ближайшего соседа, сохраняющая полезные свойства упорядоченных шкал, и доказываются соответствующие теоремы (Теоремы 4.3.1 и 4.3.2). Далее, в 4.3.3. предлагается эмпирический метод модификации правила ближайшего соседа.

4.3.1. Бинаризация признаков

Последовательность проверки граф-схемой признаков чрезвычайно сильно влияет на результат обобщения. Это видно из метрики d, в которой первый признак перевешивает все остальные. Далеко не всегда информативность признаков расходится столь сильно. Чаще признаки почти равноправны. Одним из примеров такой ситуации является евклидова метрика области значений признаков. Бинаризация позволяет сгладить неравноправность признаков.

Рассмотрим признак x_i с областью значений D_i. Так как D_i конечно, мы можем занумеровать все элементы D_i. При этом, если D_i упорядочено, то желательно, чтобы номера элементов D_i следовали этому порядку. Введем n=log|D_i| новых признаков: x_i1, x_i2,.., x_in. Причем, x_ik представляет собой k-й разряд двоичного представления номера значения признака x_i:

где #d_i- порядковый номер d_iD_i, [·] - операция взятия целой части.

Очевидно, что подпространство признака x_i: _i эквивалентно подпространству описаний признаков {x_ik}:

x_i:[0,1]^Ω→[0,1]^Di

x_ik:[0,1]^Ω→[0,1]^Dik  , где D_ik={0,1}

Таким образом, признак x_i можно заменить набором двоичных подпризнаков {x_ik} следующим образом:

и

будет эквивалентно

и

Классифицируемый объект y, как и ранее преобразуется ко множеству почти четких y_d:

каждое из которых, с учетом бинаризации признака x_i примет вид:

Если обучения для необходимостей не предполагается, то бинаризация их не имеет особого смысла.

В силу эквивалентности обучающих множеств бинаризацию можно проводить для всех признаков. Поэтому для того, чтобы сделать признаки x₁ и x₂ более или менее равноправными их, можно бинаризовать и перемешать полученные бинарные признаки:

4.3.2. Линейно-упорядоченные признаки

Если множество значений признака x_i обладает естественным линейным порядком, т.е. a,b,cD_i

1. a a

2. a b a a = b

3. a b c a c

4. a b V a b , то

такой признак мы будем называть линейно-упорядоченным. Область значений D_i линейно-упорядоченного признака x_i является шкалой порядка [Хан78].

Операция бинаризации признака x_i вводит на D_i метрику d'_i:

которая может не совпадать с естественной метрикой d_i в том смысле, что точки, ближайшие по d_i и d'_i к некоторой другой точке D_i, могут оказаться различными. Например, если D_i есть натуральные числа {1,2,3,4,5}, то согласно d'_i 1 ближе к 5, чем к 4:

d'_i(1,5) = d'_i(0012,1012) = 4 < 5 = d'_i(0012,1002) = d'_i(1,4).

Если считать, что метрика линейно-упорядоченного признака должна быть согласована с отношением порядка, т.е.

a_i,b_i,c_iD_i  a_ib_ic_i  d_i(a_i,b_i) d_i(a_i,c_i) ,

то требование совпадения естественой метрики и метрики бинаризованных признаков можно ослабить до требования согласованности последней с отношением порядка.

Такой согласованной метрикой является d^*_i:

.

Прежде всего покажем, что d^*_i действительно удовлетворяет аксиомам расстояния:

1. d^*_i(a_i,b_i) = 0 a_i=b_i

2. d^*_i(a_i,b_i) = d^*_i(b_i,a_i)

3. d^*_i(a_i,c_i) + d^*_i(c_i,b_i) =

= d^*_i(a_i,b_i)

Теорема 4.3.1. (доказательство)

Для произвольного подмножества A_iD_i и некоторого a_iA_i, если å_iA_i- ближайший по d^*_i к a_i элемент A_i, то среди всех элементов A_i:

1. å_i совпадает с a_i в наибольшем числе первых бинарных признаков (разрядов) x_ik.

2. Если первый несовпадающий разряд a_in= 0, то среди разрядов å_in+1, å_in+2,... наибольшее число первых нулей.

3. Если a_in= 1, то среди å_in+1, å_in+2,... наибольшее количество единиц.

Теорема 4.3.2. (доказательство)

a_i,b_i,c_iD_i

a_ib_ic_i  d^*_i(a_i,b_i) d^*_i(a_i,c_i)

Требование согласованности не обеспечивает совпадения метрик d_i и d^*_i, но согласно доказанной теореме гарантирует, что

a_ib_ic_i  d^*_i(a_i,b_i) d^*_i(a_i,c_i)

Таким образом, бинаризация линейно-упорядоченного признака с учетом метрики d^*_i не слишком сильно изменит характер обучения. Применение более сильных шкал, например шкалы интервалов [Хан78], видимо слишком ограничивает эффективность обучения. Кроме того, методы классификации для евклидовых пространств признаков достаточно хорошо разработаны [Хан78, Фук79, Ту78].

Рассмотрим те изменения, которые следует внести в алгоритм построения граф-схемы для реализации метрики d^*_i. На шаге 6.a алгоритма узел не генерировался, что приводило к тому, что значение признака, который мог бы проверяться этим узлом, никак не учитывалось. Если этот признак x_in порожден бинаризацией линейно-упорядоченного признака x_i, мы теперь будем генерировать узел при условии, что x_in не покрывает всей области своих значений ({0,1}), и если в подграфе с вершиной в этом узле присутствуют узлы, проверяющие хотя бы один из признаков x_in+1, x_in+2,..., т.е. бинарных признаков, порожденных признаком x_i. Причем, возможны два варианта, в зависимости от значения признака x_in:

x_in(q)=0 , тогда дуга с весом 0 ведет в подграф с вершиной в данном узле, а дуга с весом 1 в тот же подграф, то с подставленными в качастве значений признаков x_in+1, x_in+2,... единицами.

x_in(q)=1 , тогда дуга с весом 1 ведет в этот подграф, а дуга с весом 0 в него же, но с подставленными нулями вместо значений x_in+1, x_in+2,...

Данные изменения обеспечивают согласно теореме 4.3.1 реализацию граф-схемой метрики d^*_i при условии, что порядок проверки признаков x_in+1, x_in+2,... не изменяется.

4.3.3. Граф-схема как наилучшее продолжение

Как уже отмечалось выше алгоритм построения граф-схемы обеспечивает включение непредставленных в обучающем множестве точек области значений признаков в ближайшие к ним образы классов. При этом, значение функции принадлежности включаемой точки заимствуется у ближайшей к ней точки образа класса.

Можно усовершенствовать алгоритм построения граф-схемы таким образом, чтобы значение функции принадлежности включаемой точки уменьшалось в зависимости от ее удаленности от образа класса (т.е. ближайшей к ней точки образа класса).

Предположим, что f_i- убывающая функция расстояния d_i такая, что f_i(0)=1, а f_i()=0. Тогда на шаге 6 алгоритма построения граф-схемы, когда некоторые значения признака x_i не покрываются дугами, следует включать эти значения в веса дуг со значениями функции принадлежности, домноженными на f_i от расстояния между значением и дугой. Например, если D_i={1,2,3,4}, то дуга будет преобразована, как показано на рис. 4.7.

Pис. 4.7. Преобразование дуги граф-схемы

Здесь {2:1,3:1,4:f_i(1)} обозначает нечеткое множество с функцией принадлежности, принимающей значения 0 в 1, 1 в 2 и 3, f_i(1) в 4. Точка 4 включена в дугу со значением функции принадлежности 1·f_i(4-3), где 1 - значение функции принадлежности в точке 3 - ближайшей к 4 точке D_i.

Граф-схема, полученная с помощью данного алгоритма уже не будет четкой для признаков x₁,...,x_N, однако при преобразовании классифицируемого объекта к четкому виду классификация остается поиском пути в четком графе.

4.3.4. Преобразование вероятностных данных

Часто бывает так, что значения признака x_i задаются в виде распределения вероятности. Т.е. в качестве исходных данных мы располагаем функцией P_i(·|p). Где P_i(·|p) есть условное распределение вероятности над множеством значений признака x_i нечеткого события p. Иначе говоря, d_iD_i P_i({d_i}|p)=P_p(d_i) - вероятность того, что признак x_i принимает значение d_i на нечетком событии p. Величины P_p(d_i) могут быть получены, например, как относительные частоты появления значений d_i или методами статистического оценивания.

В подобных случаях перед нами стоит задача получения по P_p образов нечетких событий p и . Или, другими словами, задача построения функции распределения возможности по функции распределения вероятности. Этот вопрос рассматривается в [Дю90, Бор89], поэтому мы изложим лишь основной результат.

В качестве распределения возможностей x_i(p) можно взять нечеткое множество _F* [Дю90]:

А в качестве распределения необходимостей

[Дю90]:

Например (рис. 4.8.), если множество значений признака есть D_i={1,2,3,4}, а P_p(1)=0, P_p(2)=0.2, P_p(3)=0.5, P_p(4)=0.3.

Рис. 4.8. Преобразование распределения вероятностей в распределение возможностей и необходимостей

4.3.5. Получение возможностей из экспертного опроса

Существует обширная литература, посвященная вопросу построения функции принадлежности нечеткого множества по данным опроса экспертов [Яг86, Мел90, Мал91]. Мы изложим лишь простейший способ получения x_i(p), так как в большинстве приложений признаки оцениваются без участия человека.

Пусть n экспертов утверждают, что значение d_i признака x_i реализуется на предъявленном им нечетком событии p, а m экспертов придерживаются противоположного мнения, тогда можно принять, что

Аналогичным образом эксперты опрашиваются и по поводу .

4.3.6. Предобработка исходных данных

Исходные признаки часто имеют непрерывные области значений. В этом случае, а так же, когда мощность области значений слишком велика, необходимо выполнить дискретизацию области значений признака. Подобного рода предобработка является типичной задачей кластеризации [Кла80]. Целесообразно, в данном случае, применять наиболее простые алгоритмы кластеризации, например гистограммные методы или методы, описываемые в [Каз88а, Каз88б], так как основная задача предобработки - понижение мощности пространства описаний с наименьшими потерями в разделимости классов. Эта задача может оказаться достаточно трудной для зависимых признаков, когда границы кластеров становятся подвижными. Интересным, в таких случаях, представляется применение техники нечеткого кластер анализа [Bez91]. При этом область значений признака покрывается набором нечетких интервалов - аналогов фокальных элементов теории Демпстера-Шейфера, а одно и тоже значение признака может входить с различными степенями уверенности в несколько интервалов-кластеров.

Проблема предобработки усложняется, когда значения признаков случайны. Постановка задачи нечеткого обучения подразумевала, что неопределенность значения признака оценивалась источником, из которого это значение поступало. Типичный пример, когда человека просят определить на глаз высоту дерева, а он отвечает - «метров десять», что предполагает некоторый нечеткий интервал с центром в точке десять. Иная ситуация возникает, когда признаком является, например, масть выпавшей карты. Если распределение плотности вероятности априорно известно, то оно может быть преобразовано к распределению возможностей, описанным ранее способом. Однако, чаще всего, его приходится оценивать по обучающей выборке, что весьма не просто сделать в условиях зависимости признаков, малого объема выборки и неизвестных априорных вероятностях классов. Наиболее простым выходом из подобной ситуации является оценка вероятностей принадлежности классам только для тех обучающих примеров, которые встречаются в обучающем множестве несколько раз, входя при этом в различные классы. В предположении равных априорных вероятностей классов, все совпадающие по дискретизованным значениям обучающие примеры, заменяются на один новый пример, в котором вероятности его принадлежности классам приравниваются относительным частотам их появления в замещаемом наборе примеров. Далее это распределение вероятностей преобразуется к распределению возможностей и необходимостей обычным способом.

4.4. Дообучение

В данном разделе будет рассмотрена проблема дообучения с использованием нечетких граф-схем. Предлагается алгоритмы дообучения и изменения порядка проверки признаков граф-схемой.

Реальная обучающаяся система существует в некотором временнóм интервале, в течение которого возможно появление новых обучающих примеров, хотя бы в силу ограниченности машинных ресурсов, не позволяющих обрабатывать обучающие множества слишком большого размера. Существуют и другие причины, по которым желательно предусмотреть возможность дообучения. Отметим, что в данном случае, речь пойдет только о дообучении, но не о переобучении. Разница между которыми состоит в том, что при дообучении считается, что классы и признаки не претерпели изменений по прошествии времени с момента последнего вмешательства в систему, т.е. новые обучающие примеры могут отвергать лишь обобщения, сделанные на основе предыдущего обучающего множества, но не его само. При переобучении допускается изменение классов и признаков и, соответственно, возможно отвержение ранних обучающих примеров.

В качестве исходных данных дообучения выступает новое обучающее множество L и граф-схема G, построенная по старому обучающему множеству.

Пусть некотрое d представлено в L. Тогда L задает для такого d распределение возможностей и необходимостей его принадлежности классам p_j: (d) и (d), где

взяты из правила типа «перечисления», построенного по L.

С другой стороны, G некоторым образом классифицирует точечные множества

причем имеет место следующая ситуация

Задача дообучения - устранить данное противоречие.

Рассмотрим граф-схему возможностей G_C. При данном d существует единственный путь в четкой ее части, проверяющей признаки с x₁ по x_N. Возможны две ситуации:

1. Признак x_N+1 проверяется при классификации (рис.4.9.)

Рис.4.9. Путь, проверяющий признак x_N+1

2. Признак x_N+1 не проверяется (рис. 4.10.)

Рис.4.10. Путь, не проверяющий признак x_N+1

Таким образом, при фиксированном d граф, получаемый из граф-схемы возможностей не ветвится вплоть до проверки признака x_N+1. Пусть неветвящаяся часть пути есть T, а его длина r. Рассмотрим два случая:

r=N-1, т.е. вдоль пути T проверяются все признаки, от x₁ до x_N. Следовательно, их значения в старом обучающем множестве нам известны - это веса дуг p₁, p₂,... И i d_ip_i - d_i входит в дугу.

r<N, т.е. часть признаков не проверяется. Предположим, что значения непроверяемых признаков были тем или иным способом сохранены. Если среди непроверяемых признаков есть хотя бы один x_k такой, что d_kD_k, это означает, что d не было представлено в старом обучающем множестве. В этой ситуации нужно найти наибольшее k при котором d_kD_k (т.е. как можно дальше отойти от корня граф-схемы), создать на пути T узел, проверяющий признак x_k и присоединить к нему узел, проверяющий вырожденный признак x_N+1 (рис. 4.11.).

Рис. 4.11. Модификация пути граф-схемы

Если же для всех i d_ip_i, то d было представлено в старом обучающем множестве. Следовательно, исходя из принципа дообучения, необходимо изменить веса дуг узла, проверяющего признак x_N+1, в ситуации 1 или создать таковой в 2. Причем вес дуги, ведущей в класс p^j - w_j корректируется следующим образом:

w_j = max [w_j, (d)]

Следует ометить, что если через изменяемый узел проходят кроме T другие пути, то необходимо создать для них его неизмененную копию. Линейная упорядоченность признаков при создании нового узла должна учитываться обычным образом.

Проделав эту операцию для всех d, представленных в новом обучающем множестве, следует объединить совпадающие узлы, просмотрев все новые и измененные узлы.

Граф-схема необходимостей корректируется тем же способом, за исключением того, что веса дуг корректируются в сторону уменьшения:

w_j = min [w_j, (d)]

Рассматривая работу данного алгоритма для обучающего множества, состоящего из единственного точечного обучающего примера, можно убедиться в справедливости нижеследующей теоремы.

Теорема 4.4.1.

Граф-схема, полученная при помощи дообучения, не отличается от граф-схемы, построенной по обучающему множеству - объединению старого и нового обучающих множеств.

4.4.1. Селекция признаков

Результат обучения в очень большой степени зависит от порядка проверки признаков. Общим правилом является желательность проверки признаков в порядке убывания их информативности [Орл82]. Задача определения информативности признаков по обучающей выборке чрезвычайно сложна даже в том случае, когда признаки суть случайные величины.

Поэтому вместо строгого определения понятия информативности признака разумно воспользоваться эмпирическими характеристиками сложности граф-схемы. Такими как:

• общее количество узлов,
• количество узлов данного уровня (проверяющих данный признак),
• насыщенность узлов - количество исходящих из них дуг,
• степень дихотомии узлов - мощность наибольшего из множеств попарных пересечений весов дуг, исходящих из данного узла.

и.т.п. А для их оптимизации применить технологию экспертных систем.

Важным вопросом, в этой связи, становится задача изменения порядка проверки признаков. Трудно сказать, что является менее накладным с точки зрения расходов машинного времени - построение новой граф-схемы по старому обучающему множеству, с учетом изменения порядка проверки признаков, или корректировка уже существующей ее версии.

4.4.2. Изменение порядка проверки признаков

Рассмотрим случай, когда необходимо изменить порядок проверки признаков x_i и x_i+1 на обратный. Имея данную операцию в качестве примитива, мы можем получить произвольную последовательность проверки признаков.

Поскольку алгоритм сходен для граф-схем возможностей и необходимостей, рассмотрим только первую из них.

Выделим в граф-схеме возможностей часть, проверяющую признаки x_i и x_i+1 (рис. 4.12.).

Рис. 4.12. Часть граф-схемы возможностей

Сразу исключим из рассмотрения те входящие дуги, которые сразу ведут в узлы, проверяющие признак x_i+1, и те, на пути по которым после проверки признака x_i не делается проверка x_i+1.

Рассмотрим пути, начинаемые оставшимися входящими дугами. Например, рассмотрим часть граф-схемы, показанную на рис. 4.13.

Рис. 4.12. Часть граф-схемы, подлежащая преобразованию

Построим обучающее множество в котором дуги t₁...t_l играют роль классов, а новый признак x₀ принимает значения из s₁...s_k. Каждый путь по s_n в t_m в новом обучающем множестве получает обучающие примеры, приведенные на рис. 4.14.

Рис. 4.14. Обучающее множество для преобразования граф-схемы

В которых в качестве значений признаков x_i и x_i+1 стоят веса соответствующих дуг. Если признак x_i+1 не проверяется на пути по s_n в t_m, то остальные обучающие примеры для путей по s_n дополняются примерами с соответствующими значениями x_i и p_j. Например, рассмотрим часть граф-схемы. приведенную на рис. 4.15.

Рис. 4.15. Пример преобразования граф-схемы

Так как δε=ζη=D_i+1, то непосредственное построение по новому обучающему множеству обновленной части граф-схемы приведет к пересекающимся весам дуг: δζØ V δηØ, что нежелательно. Поэтому по δ, ε, ζ, η следует построить порождающие элементы {λ_k} такие, что с помощью их объединений можно получить δ,...,η. Делать это нужно для каждой уникальной дуги s_n. Далее каждый обучающий пример расщепляется на соответствующее число новых обучающих примеров по количеству λ_k входящих в вес дуги из узла, проверяющего признак x_i+1. Например, если D_i+1={0,1,2}; Di={0,1,2,3} и то λ_k для {0},{1,2,3},{0,1},{2,3} есть {0},{1},{2,3}. Соотвествующая граф-схема, обучающее множество и процесс построения эквивалентной ей граф-схемы с другим порядком проверки признаков приведены на рис. 4.16.

Рис. 4.16. Конкретная граф-схема

В итоге мы получим новую часть граф-схемы возможностей, приведенную на рис. 4.17.:

Рис. 4.17. Новая граф-схема возможностей

Процесс изменения граф-схемы необходимостей проходит таким же образом, за исключением того, что λ_k строятся как набор множеств, позволяющий получать веса дуг путем их пересечений, а не объединений, как в случае граф-схемы возможностей.

4.5. Пример построения нечеткой граф-схемы возможностей

Пусть обучающее множество содержит шесть обучающих примеров: q₁,...,q₆. Для каждого из которых задано нечеткое множество x(q_i) над областью значений двух линейно-упорядоченных признаков: x₁ и x₂, принимающих значения из {0,1,...,7}. Кроме того, для каждого обучающего примера задано распределение возможностей принадлежности его трем классам: p¹, p² и p³ - C_q. Мы изобразим это графически (рис. 4.18.):

Рис. 4.18. Обучающее множество

Здесь степени принадлежности данной точки области значений признаков обозначены яркостями (рис. 4.19.):

Рис. 4.19. Уровни принадлежности

Признаки x₁ и x₂ мы бинаризуем: x₁→x₁₁x₁₂x₁₃; x₂→x₂₁x₂₂x₂₃ и перемешаем полученные признаки, таким образом, что они будут проверяться в последовательности: x₁₁x₂₁x₁₂x₂₂x₁₃x₂₃. Для того, чтобы привести задачу к стандартному виду, введем дополнительный признак x₃ с областью значений {1}, и приведем обучающее множество к четкому по признакам x_ij виду. В качестве порога T выберем 0.5.

В представленной на рис. 4.20. таблице в первом столбце находятся обучающие примеры нового обучающего множества. Во втором столбце - распределение возможностей принадлежности обучающего примера классам. В третьем - веса дуг узлов граф-схемы, проверяющих признак x₃, равные произведению возможности принадлежности данного обучающего примера классу, в который ведет дуга, на возможность принадлежности данной точки области значений признаков x₁, x₂ обучающему примеру. В четвером - метки соответствующих узлов. На рис. 4.20. показан так же первый шаг алгоритма построения граф-схемы. На нем слева находится таблица для обучающего множества, справа - ее преобразование на первом шаге алгоритма построения граф-схемы возможностей. Рамками обозначены классы эквивалентности обучающих примеров. Фигурными скобками - соответствующие им названия генерируемых узлов граф-схемы.

Рис. 4.20. Построение граф-схемы (первый шаг)

Далее приводится последовательность выполнения шагов алгоритма построения граф-схемы возможностей. Квадратными рамками обведены классы эквивалентностей. Фигурные скобки указывают на соответствующие классам эквивалентности узлы. Звездочкой отмечаются узлы, для которых требуется учтывать линейную упорядоченность. Например, узел K, проверяет признак x₂₃, но на шаге n=4 проверка признака x₂₂ не потребовалась, поэтому при классификации, если x₂₂0, то x₂₃ следует считать равным 1. Последовательность следующих шагов построения граф-схемы приведена на рис. 4.21.

Рис. 4.21. Построение граф-схемы

Полученная граф-схема возможностей содержит 6 четких слоев, проверяющих признаки x₁₁x₂₁x₁₂x₂₂x₁₃x₂₃, и один слой, проверяющий вырожденный признак x31. Результат ее построения приведен на рис. 4.22.

Рис. 4.22. Граф-схема возможностей

Далее мы приводим результат классификации всех точек области значений признаков, т.е. нечеткие множества p¹_С, p²_С, и p³_С, представляющие собой распределение возможностей принадлежности точек области значений признаков классам p¹, p² и p³, соответственно (рис. 4.23.).

Рис. 4.23. Образы классов, порождаемые граф-схемой

Где степени принадлежности точек области значений признаков обозначены яркостями, приведенными на рис. 4.19. Например, точка (4,4) принадлежит p¹ с возможностью 1; p² - 0.6 и p³ - 0.

4.6. Выводы

1. Нечеткие граф-схемы являются удобным средством представления нечетких классификаторов.

2. Для машинной реализации разумно использовать граф-схемы в канонической форме - с четкими дугами.

3. Алгоритм построения граф-схемы реализует нечеткое правило ближайшего соседа.

4. Бинаризация признаков может быть выполнена с сохранением полезных свойств упорядоченных шкал признаков. При этом, признаки могут быть сделаны почти равноправными.

5. Дообучение и изменение порядка проверки признаков могут быть выполнены без полной перестройки граф-схемы.

to chapter five