Теорема 4.3.1.

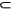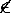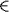Для произвольного подмножества A_iD_i и некоторого a_iA_i, если å_iA_i- ближайший по d^*_i к a_i элемент A_i, то среди всех элементов A_i:

1. å_i совпадает с a_i в наибольшем числе первых бинарных признаков (разрядов) x_ik.

2. Если первый несовпадающий разряд a_in= 0, то среди разрядов å_in+1, å_in+2,... наибольшее число первых нулей.

3. Если a_in= 1, то среди å_in+1, å_in+2,... наибольшее количество единиц.

Доказательство:

1. 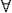k<n a_ik = å_ik d^*_i(å_i,a_i) = 

Следовательно, один разряд перевешивает вклад всех последующих.

2. Если a_in= 0; å_in = 1, то

d^*_i(å_i,a_i) =

Отсюда у å_i должно быть наибольшее количество первых нулей после å_in для того, чтобы вклад второго слагаемого модуля был наименьшим (отрицательным).

3. Если a_in= 1; å_in= 0, то

d^*_i(å_i,a_i) =

Следовательно, у å_i должно быть наибольшее количество первых единиц после å_in, что сделает второе слагаемое максимальным.

q.e.d.