![[Home]](home.jpg){kind=small}
Fuzzy graph-schemes in pattern recognition © 1992 Dmitry A.Kazakov
1. Концепция нечеткости
Понятие нечеткости интуитивно понятно каждому человеку, но его формализация всегда вызывала трудности. Долгое время считалось: все что требуется для работы с неопределенностью это теория вероятностей. Однако, по мере того, как в область наших интересов стали попадать вопросы, связанные с восприятием мира живыми существами и, в частности, человеком (В основном это относится, конечно к работам в области искусственного интеллекта) адекватность теории вероятностей начала вызывать сомнения. В практических работах стали использоваться эмпирические модели заменяющие вероятностную меру ее суррогатами. Здесь достаточно упомянуть факторы уверенности в экспертной системе MYCIN [Mak83, Экс87, Zho88, Уот89]. Тем временем в теоретическом плане благодаря работам Заде (Zadeh), Шейфера (Shafer) и др. была достигнута некоторая ясность.
Говоря об источниках неопределенности Бездек (Bezdek) перечисляет следующие [Bez81]:
Гупта (Gupta) в [Gup88] классифицирует неопределенность следующим образом:
Дюбуа (Dubois) и Прад (Prade) в [Дю90] связывают нечеткость с неопределенностью разбиения пространства элементарных испытаний и нечеткостью квалификаторов естественного языка (типа приблизительно, очень и т.п.). Таким образом, современное представление о неопределенности не сводится к случайности - неопределенности первого рода в классификации Гупты. В чем заключается эта несводимость?
Если мы возьмем типичный нечеткий предикат высокий человек, то в принципе существуют две школы, пытающиеся выразить его в терминах вероятности.
Первая из них извлекает случайность из внешнего мира. Степень истинности предиката высокий человек. принимается равной вероятности того, что некто, случайно выбранный наблюдатель, скажет про интересующего нас человека, что он высок. Исходя из этого предположения можно построить функцию принадлежности нечеткого множества высоких людей путем экспертного опроса. Однако основной постулат на котором эти действия базируются - вся неопределенность заключается в том, что разные люди думают по-разному - явно неверен, ибо даже один человек никогда не даст точного ответа. Поэтому вторая школа объясняет неопределенность вероятностным характером восприятия и мышления человека. Но очевидные в этом случае действия - показывать одного и того же человека одному наблюдателю несколько раз обречены на провал. Суть проблемы в том, что на вопрос, что же является пространством элементарных событий, нельзя дать удовлетворительный ответ в том смысле, что не существует объектов реального мира, с которыми мы могли бы отождествить элементарные события.
Все, что мы можем сделать это предполагать, что за каждым нечетким событием стоит совокупность вполне определенных событий (не обязательно случайных), но выяснить какое из них происходит мы не можем [Дю90]. Эта ситуация замечательным образом напоминает теорию неизвестного параметра в квантовой физике. В конце концов физики от нее отказались приняв, что частицы действительно ведут себя случайным образом [Фей65].
Отодвинув философские аспекты данного вопроса на задний план мы принимаем концепцию нечеткого события либо как удобную абстракцию, либо как реально существующую вещь. Таким образом, предикат высокий человек может быть выражен функцией принадлежности нечеткого множества высокие люди. Неопределенности первого и второго рода могут смешиваться, как например в: во второй половине дня пойдет дождь. Здесь есть и нечеткость: вторая половина дня, дождь и случайность, связанная с недостаточным знанием механизма возникновения дождя.
1.1. Меры неопределенности
Приняв концепцию нечеткости мы сталкиваемся с вопросом количественного выражения нечеткости. Другими словами, необходимо определить алгебру нечетких множеств и нечеткую меру.
Прежде всего, следует задать область значений функции принадлежности нечеткого множества. Обычно, так же как это сделал Заде в 1965 году, считается, что уровни принадлежности принимают значения из интервала [0,1]. Однако, возможны и более общие определения. Например, гипернечеткие множества, значения функции принадлежности которых есть нечеткие числа [Коф82, Ав86, Дю90].
Далее необходимо рассмотреть интуитивно очевидные свойства нечетких множеств. Не вызывает сомнения, что множество нечетких подмножеств должно обладать свойствами дистрибутивной решетки [Bez81, Коф82, Дю90]:
Операции объединения
и пересечения
нечетких
множеств удовлетворяют требованиям:
Операция дополнения нечеткого множества, обладающая свойствами:
Коммутативности: A A Ассоциативности: (A (A Идемпотентности: A A Поглощения: A A Дистибутивности: A A
делают множество нечетких подмножеств решеткой де Моргана. Справедливо следующее утверждение: единственными операциями объединения и пересечения, порождающими решетку де Моргана для нечетких подмножеств, являются операции max и min (теорема Беллмана-Гертса). Существуют и другие операции объединения и пересечения, удовлетворяющие той или иной части свойств решетки де Моргана [Три86, Бор89, Дю90]. В работе [Три86], в частности, рассматриваются интерестные свойства операций дополнения не обладающие качеством инволюции. Однако в целом можно сказать, что связки max и min, как их ввел Заде, оказались наиболее продуктивными для определения операций объединения и перечесения нечетких множеств.
Инволюции: Теоремы де Моргана: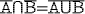 
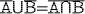
Еще один вопрос, который возникает в связи с мерой нечеткости, это - откуда взять величины уровней принадлежности и как их измерить? Многие критики теории нечетких множеств справедливо отмечают, что не существует удовлетворительного способа определения уровней принадлежности. Но при этом, не упоминается, что в точности та же проблема существует и в теории вероятностей - определение вероятности как предела отношения частот некорректно ибо этот предел не существует в строгом смысле. Имеется лишь слабая сходимость - сходимость по вероятности. Т.е. налицо типичный порочный круг - вероятность определяется через вероятность. Подробное обсуждение этого вопроса можно найти у Литлвуда (Littlewood) в [Лит65]. Тем не менее, это не мешает нам пользоваться теорией вероятности и математической статистикой. Что касается практического измерения и оценки уровней принадлежности, то в настоящее время этот вопрос детально разработан. Достаточно сослаться на работы [Тан74, Яг86, Куз86, Нор86а, Нор86б, Бор89, Дю90, Мал91].
1.2. Нечеткие события
Реально в каждом событии неопределенность наличиствует в двух ипостасях: случайности и нечеткости. Таким образом, речь идет о нечетких случайных событиях. Понятие нечеткого случайного события, как его ввел Заде, интуитивно очевидно: нечеткое событие есть нечеткое подмножество пространства элементарных событий. Следует заметить, что так же как и для четких случайных событий, необходимо налагать некоторые ограничения на подмножество. Обычно это требование измеримости функции принадлежности нечеткого подмножества. Естественно, что определив понятие нечеткого события мы должны ответить на вопрос о его мере. Эта проблема сейчас активно разрабатывается и мы приведем основные подходы к ее разрешению.
1.2.1. Теория нечеткой меры
В рамках этого подхода ряд авторов пытается обобщить теорию меры на нечеткие множества. Основные положения были предложены Заде в 1969 году. Он определил вероятность нечеткого события A как:
A - функция принадлежности нечеткого события, а μ -вероятностная мера. При этом функция принадлежности должна быть измерима для существования интеграла Лебега. Клемент (Klement) в фундаментальной работе [Kle80] ввел определение нечеткой σ-алгебры и четко-значной нечеткой меры, удовлетворяющей требованию:
, где
Несколько более общий подход, базирующийся на понятии нечеткого измеримого пространства рассматривался в [Ska88]. Нечеткое измеримое пространство замкнуто относительно дополнения и счетного числа объединений и пересечений. На нем автор рассматривает ряд функционалов, обладающих желаемыми свойствами.P(A
Другой подход развивается на базе теории нечетких интегралов Суджено (Sugeno) [Sug72, Цук86]. Определяемая на его основе λ-нечеткая мера обобщает вероятностную и возможностную меры (при различных значениях параметра λ, λ-нечеткая мера может вести себя как вероятность, возможность или необходимость). λ-мера ослабляет требование аддитивности до:
На базе λ-нечеткой меры можно определить нечеткое ожидание (fuzzy expected value) и строить нечеткий аналог математической статистики [Ав86, Sch87].P(A
Однако при всей своей привлекательности
теория нечеткой меры вызывает серьезные возражения, вытекающие из очевидного
соображения - если событие нечетко, то его мера должна быть нечетким
подмножеством
интервала [0,1]
(т.е.
нечетким числом), так как не известно
точно, какой именно набор
элементарных событий имело место. Впервые на этом настаивал Заде в работе
[Zad76].
Здесь нужно отметить работы Хеле (Hoele),
предложившего нечетко-значные меры [Hoh81],
т.е. меры значениями которых являются нечеткие числа. Хеле определил нечеткие
положительные числа, через нечеткие отношения
.
Таким образом, значение функции принадлежности нечетко-значной меры P
нечеткого
события A
в
точке r
([0,1]
-
величина P(A)(r)
определяет
возможность того, что вероятность A
не
превосходит
r.
Клемент в [Кле86]
подробно
рассматривает связь между четко- и нечетко-значными мерами. К сожалению,
нечеткие числа Хеле не являются нечеткими числами в общепринятом [см.
например Buc88, Ker88, Дю90].
В частности, отсутствует информация о поведении значения нечеткой меры
справа, так как в определении идет речь о неравенстве
,
а не
. Можно использовать
меру Клемента для A и его дополнения
в
качестве верхней и дополнения нижней вероятностей в теории Демпстера-Шейфера
или как возможность и дополнение необходимости в теории возможностей, которые
мы обсудим позже.
В целом можно сказать, что вопрос о построении нечеткой меры, позволяющей объединить нечеткость и случайность остается открытым.
1.2.2. Теория возможностей
Впервые меры возможности и необходимости были предложены Заде. Теория возможностей предполагает наличие распределения возможностей π над пространством элементарных событий. В отличие от теории вероятностей элементарные события рассматриваются не как непересекающиеся, но напротив, как образующие цепочку вложенных множеств. Распределение возможностей π есть нечеткое множество, функция принадлежности которого задает возможность каждого из элементарных событий. Меры возможности и необходимости некоторого нечеткого события A определяются следующим образом [Дю88, Бор89, Дю90]:
С точки зрения классификации типов неопределенности, теория возможностей пытается выразить и случайность и нечеткость в терминах только мер нечеткости и, следовательно, в этом смысле является прямой альтернативой теории вероятностей. В определении мер возможности и необходимости не проводится никакого различия между чисто случайными и чисто нечеткими описаниями. С одной стороны, это чрезвычайно удобно, так как позволяет комбинировать случайность и нечеткость в едином информационном блоке - паре возможность - необходимость. В частности, можно естественным образом представить факт отсутствия информации. С другой стороны, возможностная модель плохо работает в том случае, когда в неопределенности преобладает случайная составляющая. Тем не менее из-за того, что основные результаты теории возможностей имеют вид неравенств, она остается корректной и в этом случае, естественно, за счет огрубления результатов. По этой же причине, проблема независимости событий - камень преткновения байесовского подхода [Экс87, Пре89] - в рамках теории возможностей стоит не так остро.
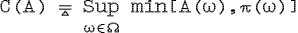
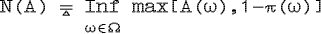
Теория возможностей тесно связана с теорией интервальных вычислений, независимо развивающейся с 1966 года [Але87] и доверительными интервалами в теоретической статистике. Так пара возможность - необходимость может рассматриваться как границы доверительного интервала [Дю90].
1.2.3. Теория Демпстера-Шейфера
Демпстер (Dempster) в 1967 году впервые ввел понятия верхней и нижней вероятности. Далее благодаря работам Шейфера была сформирована законченная теория, обобщающая стандартную торию вероятностей. Теория Демпстера-Шейфера рассматривает пространство элементарных событий структурированное в виде набора фокальных элементов. Только фокальные элементы доступны для наблюдения, тогда как элементарные события скрыты. С каждым фокальным элементом связывается опрделенная вероятность, распределение которой по элементарным событиям, составляющим фокальный элемент, не известно (ряд авторов [Дю88, Бор89] называют фокальные элементы информационными гранулами). Так как распределение вероятностей внутри фокальных элементов не известно, для некоторого события, составленного из них, можно лишь определить верхнюю и нижнюю границы допустимых значений его вероятности, названные Демпстером верхней и нижней вероятностями. В случае, когда фокальные элементы не пересекаются и покрывают все пространство элементарных событий, т.е. образуют полную группу событий, верхняя и нижняя вероятности совпадают и теория Демпстера-Шейфера превращается в стандартную теорию вероятностей. Если фокальные элементы образуют последовательность вложенных множеств, верхняя вероятность ведет себя как мера возможности, а нижняя, как мера необходимости в теории возможностей.
В рамках теории Демпстера-Шейфера находят объяснение практически все эмпирические меры доверия [Пре89, Дю90]. Причем, становятся ясными границы их применимости, что несомненно очень важно.
Дальнейшее развитие теории Демпстера-Шейфера было связано в основном с выявлением связей с теорией вероятности, теорией нечетких мер и теорией возможностей. Следует отметить работы [Гуд86, Wie88], посвященные понятию случайного множества. Случайное множество, по-аналогии со случайной величиной, определяется как измеримое отображение из одного вероятностного пространства в другое (обычно само на себя). Если для случайной величины можно определить вероятность ее принадлежности некоторому подмножеству области ее значений, то для случайного множества можно только ввести вероятности разного рода его покрытий, порождающих верхнюю и нижнюю вероятностные меры Шейфера. Вводя различные функции покрытия случайного множества авторы [Гуд86, Wie88] получают, в частности, λ-меры Суджено, меры возможности и необходимости, а так же аналоги формулы Байеса. Отметим, что проблема зависимости свидетельств при этом не снимается.
Проблемы возникают в том случае, когда события становятся нечеткими. В [Гуд86], к сожалению очень кратко, рассматривается вопрос о связи между случайными множествами и нечеткими случайными множествами. В частности показано, что нечеткое случайное множество может быть отождествлено с некоторой совокупностью четких случайных множеств. Здесь опять таки необходимо разработать теорию нечеткой меры, так как верхние и нижние вероятности будут нечеткими. Правда, они могут быть заменены некоторыми четкими верхними и нижними оценками. Таким образом мы приходим к подходу, который по сути очень близок к теории возможностей.
1.3. Выводы
1. Современное представление о неопределенности не исчерпывается категорией случайности. В задачах, тесно сязанных с человеческим мышлением и восприятием, необходимо использовать одновременно и вероятностный и нечеткий подходы.
2. Определенная близость всех трех подходов к объединению нечеткости и случайности позволяет надеятся на то, что в будущем общая теория меры неопределенности будет построена.
3. Так как на настоящий момент не существует законченной теории нечетких случайных событий, разумно использовать смешанный подход с позиций теорий возможностей и Демпстера-Шейфера.
to introduction
to chapter two